Exercises for Week 35

Hello OCaml

The primary activities for this part are the following. The order of (2) or (3) below does not matter, i.e., if you have the time to study the OCaml book before the TA class, please do so.

1. Set up the development container.

2. In-class: get familiar with the OCaml basics by studying, running (with the TA’s help), and analyzing the following examples and their reference solutions.

   • Chapter 2: date fun from https://cs3110.github.io/textbook/chapters/basics/exercises.html

     • solution: cs3110/textbook-solutions

   • Chapter 3: powerset from https://cs3110.github.io/textbook/chapters/data/exercises.html

     • solution: cs3110/textbook-solutions

   • Chapter 3: shape from https://cs3110.github.io/textbook/chapters/data/exercises.html

     • solution: cs3110/textbook-solutions

   • Chapter 4: more list fun from https://cs3110.github.io/textbook/chapters/hop/exercises.html

     • solution: cs3110/textbook-solutions

3. At-home: read-up on the supporting OCaml book chapters (Chapters 1-3, Chapter 4 if you have the time) and/or videos. (Re)-study the examples above and ask clarifications on the discussion board.

Abstract Syntax Tree traversal

In compiler implementation, it is often desired to inspect the data structures we work with. A common scenario includes working with an AST that we either process or synthesize, where we want to understand its shape. The necessary device in this case is visualization of our data structures. Oftentimes, visualization techniques we use are very rudimentary, yet it helps to be familiar with them, which is the purpose of this exercise.

We will explore two visualization approaches. In both cases, we will use the AST for arithmetic expressions from Assignment 01.

(* Defining the type for binary operations *)
type binop = Add | Sub | Mul | Div

(* Defining the type for arithmetic expressions *)
type expr 
  = Int of int                       (* Integer constant *)
  | BinOp of binop * expr * expr     (* Binary operation *)

Formatting output to console

Our first approach is to print the tree on console using indentation. Write function print_tree that when called would produce the output similar to Unix tree utility. For example, print_tree (BinOp (Add, Int 1, BinOp (Mul,  Int 2, Int 3))) would generate the output

BinOp Add
├── Int 1
└── BinOp Mul
    ├── Int 2
    └── Int 3

Hint: if you are struggling with getting the ASCII connectives right, start with a simpler version that just uses the indentation

BinOp Add
    Int 1
    BinOp Mul
        Int 2
        Int 3

Formatting to graphviz

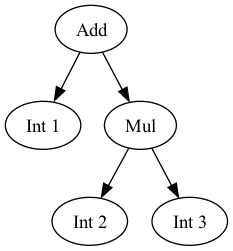
Another popular way of visualizing intermediate representations is to synthesize a .dot file to be used with Graphviz toolkit. Write a function print_aexp_to_dot that generates a .dot formatted output corresponding to the input expression. For example, for the expression above it can generate something like this

digraph AST {
  0 [label="Add"];
  1 [label="Int 1"];
  2 [label="Mul"];
  3 [label="Int 2"];
  4 [label="Int 3"];
  
  0 -> 1;
  0 -> 2;
  2 -> 3;
  2 -> 4;
}

Note that while the full spec of .dot format is quite extensive, it is sufficient to just use the basic features, such as declaration of nodes and connectives, as in the example above.

If this output is saved to a file, e.g., aexp.dot we can invoke the dot command (which is available as part of graphviz package and should be already installed in the dev container) to get an image file, e.g.,

dot -Tpng aexp.dot -o aexp.png

will generate an image as follows